Paper Summary: "Layer Normalization"

Paper Summary: "Layer Normalization"

TL;DR + Importance - We normalize the input data to stabalize and speed up training - but how? Layer norm proposses to normalize with respect to all the hidden states of a layer. This is effective in lower batch sizes + RNN's!

Abstract:

How do we speed up training? Well, we can normalize the neurons! We did this with batch normalization in the past, but the major problem with it is that it depends on the mini-batch size, plus we can't really use it for RNNs.

This paper has another normalization technique - layer normalization. Instead of normalization with respect to the mini-batch, we're just going to do it with respect to the layer! We also apply an adaptive bias and gain after normalization but before the activation function.

We do this at training and test time + we can use it with RNNs - in fact, it's super effective in RNN's and easy to implement

Introduction:

NN's take a long time to train. We can either parallelize it or make it easier for it to train. One such technique is Batchnorm, where we normalize the input data at each neuron (using mean + variance of the minibatch). NN's converge faster + it's regularization!

But Batchnorm has its problems: For RNN's the sequence length will differ, thus batch norm-ing over the batch won't be too good. We need different stats for different time steps. Plus we can't use batch norm for online learning tasks {I think this means live usage} and it can't be used for smaller batches.

This paper introduces LayerNorm - where we get the statistics through the neurons of the whole hidden layer (instead of the mini-batch). No need for it to depend on the batch size. It's good for RNNs and acts as a regularization for RNNs.

Background:

First, let's go into some definitions:

A NN takes x and maps it to y by doing this over and over again:



Primary input (a) = weight (weight) times the outputs of the previous layer (h^l). We take the primary input (a), slap a bias (b) to it, then shove it through an activation function (f) to get the outputs (h^l+1).

Notice how the primary input (not the official name by the way) is what we get after we apply the weights to the previous layer's output.

One problem we have in NN's is that gradients are highly dependent on the outputs of previous layers, thus making it all shakey (covariate shift). We don't want that because it increases training time, so we used batch norm.

What batch norm does is normalize the inputs of a hidden unit. We normalize using the mean (mu, aka the u thing) and variance (sigma, aka the o thing) of the mini-batch:



The two things on the right = fancy symbols for calculating the mean and variance of a mini-batch. On the left, we're normalizing the primary input (a) with respect to the variance and the mean. Plus we have a scaling variable (g) (officially called the gain parameter scaling).

Layer Normalization:

Since the output of one layer correlates to changes in the primary input of the next layer (especially with ReLU since it changes it a lot). Why don't we just do it over the layer (aka overall hidden states) instead of the batch?

That's what Layer normalization is:



We just compute the mean and variance over all the hidden states of a layer.

Now the entire layer will share the same mean and variance. The batches will not have the same mean and variance through (because we're re-calculating for each batch). We don't care what the batch size is, so we can use it online + with a batch size of 1.

Going back to RNN's: at test time, when we use batch norm, the statistics are fixed (we get it from training). No problem, we just store the statistics as a function of time. But what happens when we input a sequence that is longer than anything the training set has seen? Well, that's a problem!

With layernorm, we don't have that problem with RNN's since it's over the layer. Also: We're not going to calculate the primary input (a) the same as before. RNN's go unfold with time, so we'll have time instead of layer:



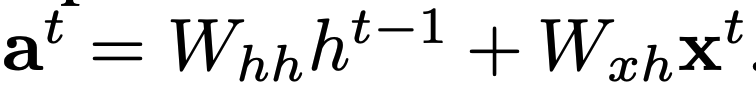
Primary input (a) = weight of hidden (W_hh) x hidden state of previous time + weight of input (W_xh) x input of current time

And we have our main calculations again, it's basically the same thing (except we have a bias (b) term added on before the activation function to get the hidden layer)



Related Work:

Batch norm of course! Another work shows how batch norm can be used in RNN (keep normalization stats for each time step + the gain parameter is best at 0.1.

There's another technique too called weight normalization. In here we don't use variance - instead, we use the L2 norm of weights to normalize our inputs.

These other models act as re-parameterizing the NN. But Layernorm doesn't do that - thus it takes the invariance problem in a different way.

Analysis:

Alright recap: All 3 norm techniques do this:



Minus mean, divide by variance - the way you normalize any data. We also add in gain (weight) and bias (bias).

Batchnorm + Layer norm get the mean + variance as we said in the above sections. For weight norm, mean = 0 and we get variance through L2 norm.



They then present this table - basically, if we're shifting X, will our Norm technique be affected?

Batch norm + weight norm = any scale to either the weight vector (individual neurons) or weight matrix (all the parameters) won't affect it at all. The mean and variance will just be scaled by the same amount, thus cancelling it out.

For layer norm, if you scale the whole weight matrix, it doesn't affect it. But if you scale an individual weight vector, it will affect it - since layer norm does it across all the weights, the weight vector will bring up, or down the mean & variance. Additionally, layer norm isn't affected by shifting the weights (re-centring) nor re-scaling of individual training cases.

[There's a ton of math that goes into the geometry of the parameter space. But it basically proves that the variance makes learning more stable]

Experimental Results:

They did experiments on 6 tasks: Image sentence ranking, question answering, contextual language modelling, generative modelling, handwriting sequence generation and MNIST classification:

Image sentence ranking:



Question answering:



Contextual language modelling:



Generative modelling:



Handwriting sequence generation:



MNIST classification:



For CNN's. It seems that batch norm still outperforms other methods. In Fully connected layers, the hidden units eahc made a similar contribution, thus we can do layer norm. But in CNN's that assumption is no longer correct, thus it's not as effective --> But next steps is to make layer norm work with CNN's.

Conclusion:

Layer normalization! We normalize with respect to the whole layer instead of batch norm. It's really good with RNN's and with smaller mini-batch sizes