What really is a Hamiltonian, linear-algebraically? Pt 2

In part 1 (which you don't need to read to understand this post), we talked about the role that a Hamiltonian plays in parametrized quantum circuits, and came to the conclusion that Hamiltonians are matrices whose eigenvector with lowest eigenvalue ("ground state") is the answer to a combinatorial optimization problem.

However, I had glossed over what a Hamiltonian really is, saying that you can use pre-built in functions to generate maxcut Hamiltonians for any graph. This time, we will dive into what Hamiltonians really are, starting with what Hamiltonian matrices took like and ending off with how you can the maxcut Hamiltonian for any graph by hand.

The Hello World of Hamiltonians

All Hamiltonians are made up of the sums of tensor products of 2x2 identity matrices and Pauli operators, which are the Pauli X, Y, and Z matrices:



A basic Hamiltonian could look something like this:



This is saying, apply the Z operator on qubit 0 and the X operator on qubit 1. To find the matrix representation, simply take the tensor product of a Z and X matrix. Here's how to do that in numpy:

Z = np.array([[1, 0], [0, -1]]) X = np.array([[0, 1], [1, 0]]) # `np.kron()` is used to take the Kronecker product, which is another word for tensor product print(np.kron(Z, X))

Out:

[[ 0 1 0 0]

[ 1 0 0 0]

[ 0 0 0 -1]

[ 0 0 -1 0]]

Congrats, you've found the matrix of your first Hamiltonian 🥳

From this example, you can see that Hamiltonians will always be square matrices whose length is equal to 2^N , where N is the number of qubits in the Hamiltonian.

A more complex Hamiltonian

Hamiltonians can have multiple terms, such as this one:



The first term is the tensor product of 2 Pauli-Z matrices, which looks like this:

[[ 1 0 0 0] [ 0 -1 0 0] [ 0 0 -1 0] [ 0 0 0 1]]

The second term is the tensor product of a Pauli-X and 2x2 identity matrix, which looks like this:

[[0. 0. 1. 0.]

[0. 0. 0. 1.]

[1. 0. 0. 0.]

[0. 1. 0. 0.]]

The resulting Hamiltonian is simply the sum of these 2 terms:

[[ 1. 0. 1. 0.]

[ 0. -1. 0. 1.]

[ 1. 0. -1. 0.]

[ 0. 1. 0. 1.]]

Because physicists and developers are lazy, it is common practice to omit writing identity operators. The above Hamiltonian will usually be written like this:



So, whenever you see a term with "missing qubits," add identity operators to each qubit that doesn't already have a X, Y, or Z operator.

Finding Hamiltonians for maxcut problems

In part 1, I showed that we can generate a maxcut Hamiltonian of any graph like this:



Now, we will look at how to calculate the maxcut Hamiltonian for such a graph by hand. (If you're unfamiliar with maxcut, read this quick 30 second explainer first.)

Forget about Hamiltonians for a second. If we want to solve a maxcut problem classically, the cost function would look like this: (picture taken from Musty Thoughts)



In layman's terms, this is what this equation is saying: for every edge with vertices i and j, the cost is 0 if both vertices are on the same side of the cut, and is the weight of the edge otherwise. z_i = 1 if vertex i is in group 0 and z_i = -1 if vertex i is in group 1.

The following table shows the final cost for each of the possible values of vertices.



Conveniently for us, this cost function can be represented as a Hamiltonian pretty easily, like this:



Where Z_i is the Z operator applied on qubit i . Notice that Z is capital this time.

Why is this the same as the previous cost function? Because the definition of Z is that the expectation value of Z on a qubit with value is |0⟩ returns 1 and the expectation value of Z on a qubit with value |1⟩ returns -1.



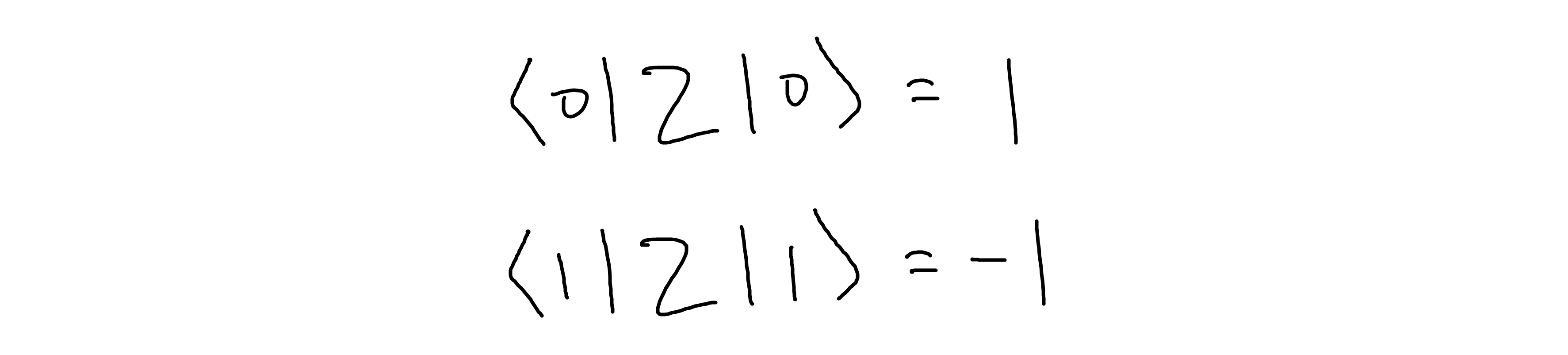
And so, using the above equation, each term of the Hamiltonian will simply be taken from each edge of the graph:



When we print out the automatically generated Hamiltonian, this is exactly what we get.

print(H)

Out:

-11.0 [] +

5.0 [Z0 Z1] +

5.0 [Z0 Z3] +

0.5 [Z1 Z2] +

0.5 [Z2 Z3]

Note: the first term has no operators which means it is an identity operator on every matrix. Identity operators don't affect quantum circuits at all.

As a challenge to you - can you convert this into a matrix? (If you can do that, you probably fully understand Hamiltonians)

Huge thanks to Michał Stęchły for explaining this to me :)