Vectorization is magical

Let's say you have some code like this.

cumulative_value = 0.0

for bitstring in expectation_values_per_bitstring:
    prob = distribution.distribution_dict[bitstring]
    expectation_value = np.exp(-alpha * expectation_values_per_bitstring[bitstring])
    cumulative_value += prob * expectation_value

final_value = -np.log(cumulative_value)

You want to apply some arithmetic operation on every element of expectation_values_per_bitstring. You might think a for loop is the a decent way to do it.

But that is wrong ❎❎❎❎❎

Instead, you can harness the power of numpy, which allows you to apply the same function to the whole array at once!

probability_per_bitstring = np.fromiter(
    distribution.distribution_dict.values(), dtype=float
)

cumulative_value = np.exp(-alpha * expectation_values_per_bitstring).dot(
    probability_per_bitstring
)
final_value = -np.log(cumulative_value)

TADA!! ✨✨✨✅✅✅

This makes a phenomenal difference in speed, which blew my socks off when I first saw it:



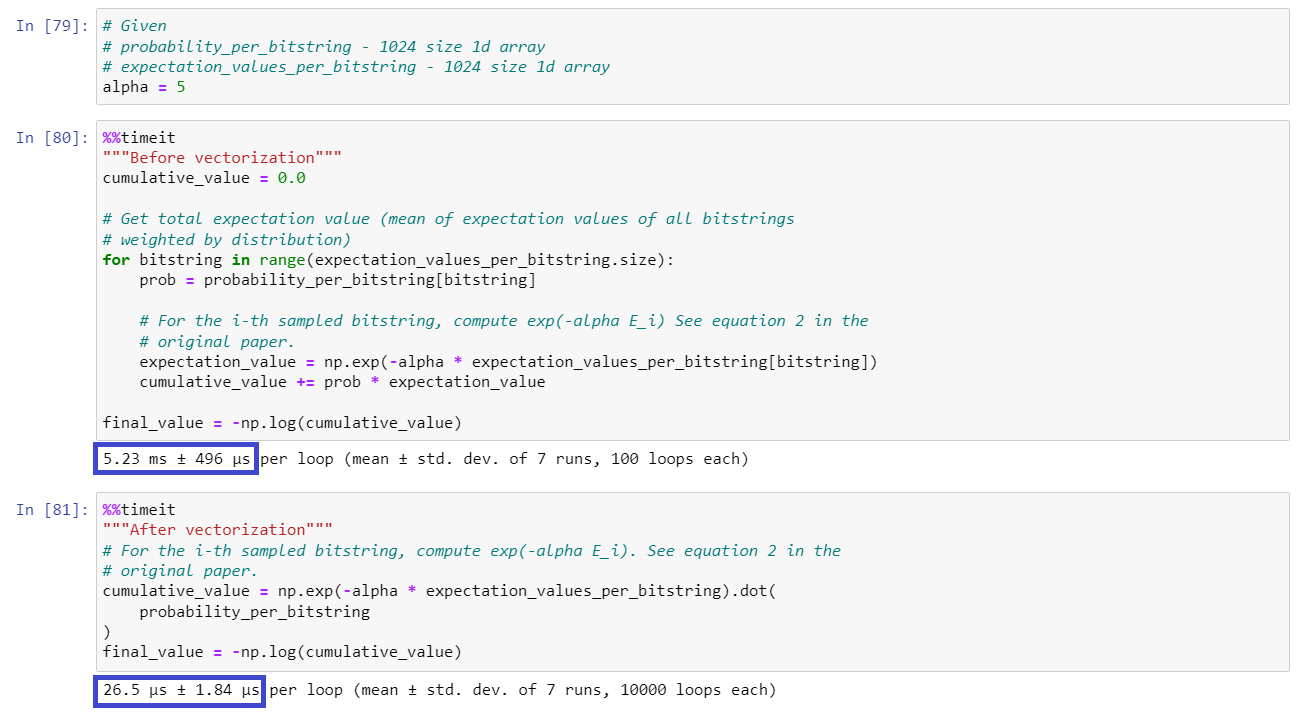
These two pieces of code do the exact same thing, but one is two orders of magnitude faster, just with a few simple tweaks. Here's the notebook if future me wants to cross reference.

This is called vectorization - applying functions to whole arrays instead of to their individual elements. Michał, a quantum software engineer at Zapata & my supervisor, told me that vectorization is a mindset. People who think in terms of it will tackle problems differnetly, and write code like 10x faster than people who think in for loops. I hope that by the end of this pseudo-blog-post, you will be on your way in harnessing the power of that mindset shift.

Here are some more examples. I will be looking through old code I wrote and roasting it.

Here, I am looping through every item in `wavefunction.amplitudes` (`2**n_qubits` is the size of `wavefunction.amplitudes`). I do an operation on each element of wavefunction.amplitudes (line 134).



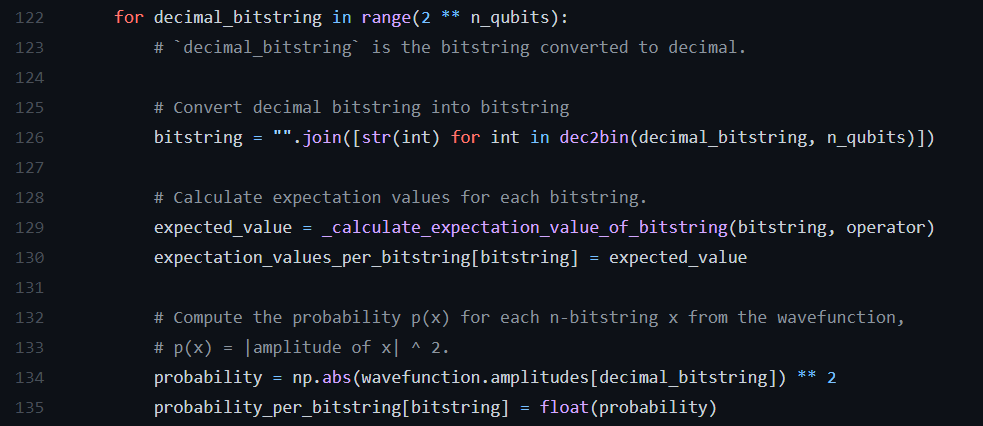
BUT wavefunction.amplitudes is already an array! Here is the better way:



Much sexier.

Vectorization rule of thumb #1: if you can avoid the for loop, avoid the for loop. They are the plague of inefficiency >:(

Here, I break up an array and use a list comprehension to apply a function on each element. Actually, I do that in two places: in both the convert and ssum functions.



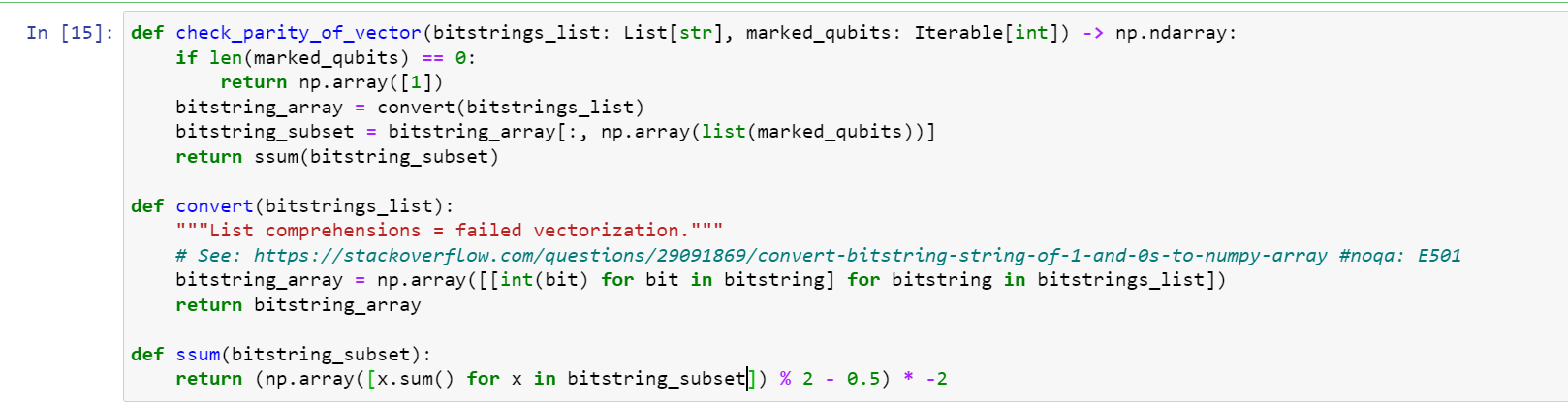
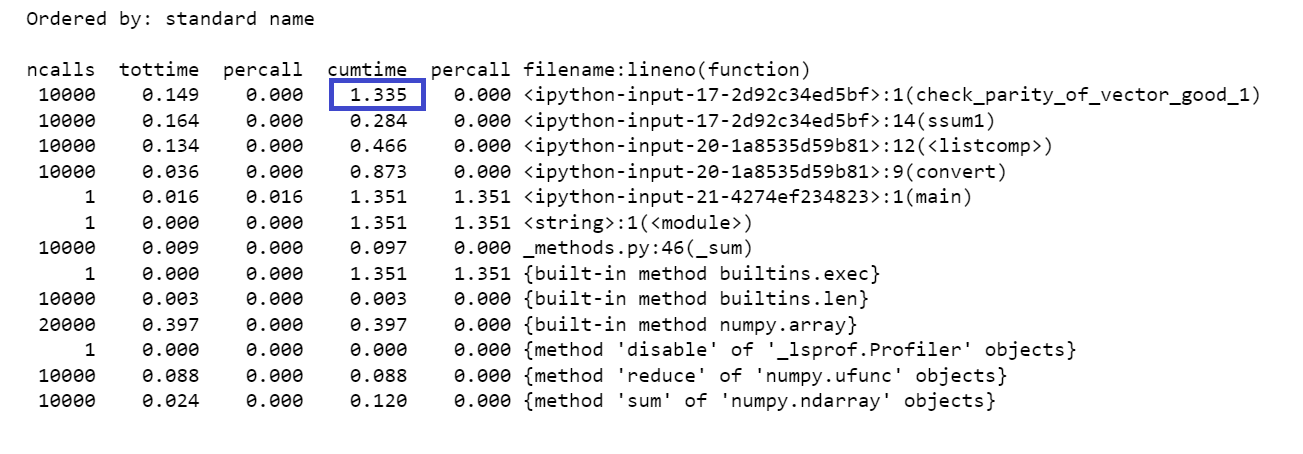
I love this example because even with complex big-matrix multiplications, two list comprehensions takes up 50% of the runtime of this function.



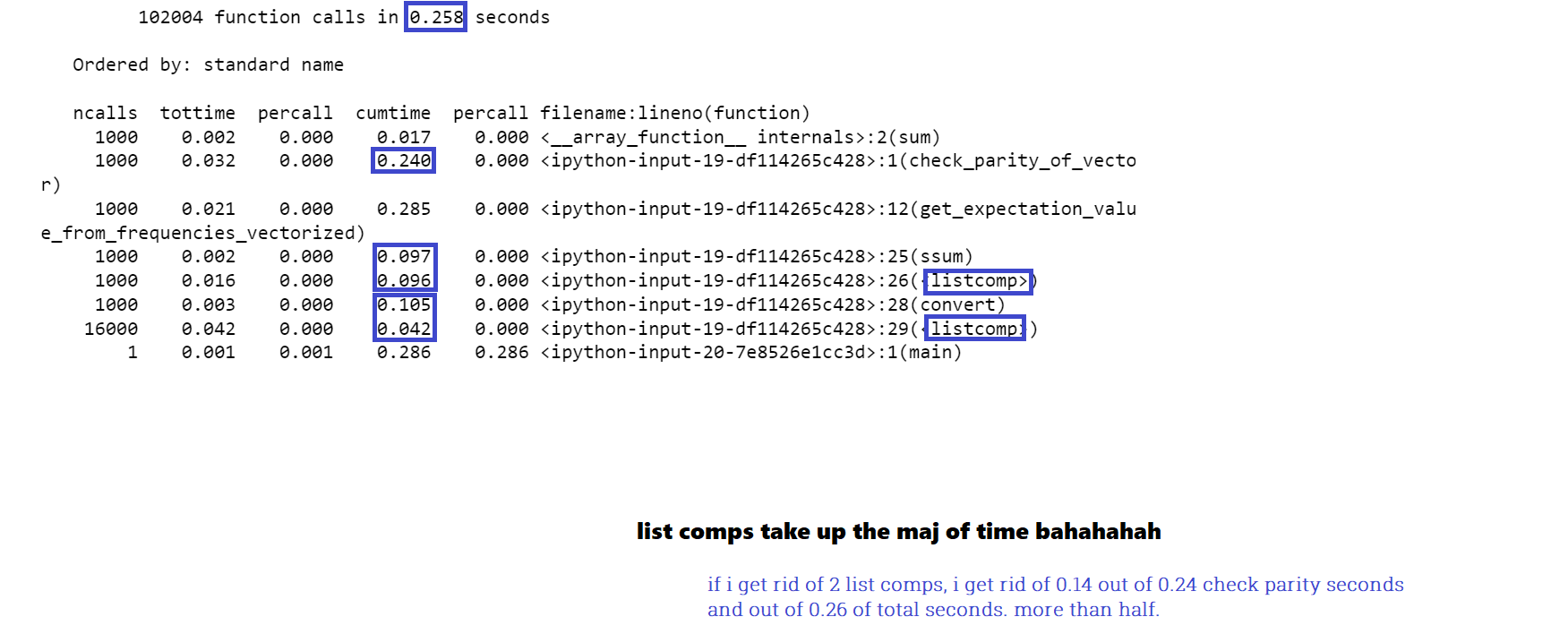
(What this says is that the total function check_parity_of_vector takes 0.24 seconds. The two list comprehensions take 0.096 + 0.042 = 0.138 seconds. That is more than half of the function's runtime. Which means I'll get a close to a 50% speedup by removing two list comprehensions.)

And them after I sacrilegiously loop through an array to make a list, I turn the list BACK INTO AN ARRAY 🤮🤮🤮🤮🤮 Quel abhor.

Vectorization rule of thumb #2: Keep numpy arrays as arrays whenever possible. As this stackoverflow post shows, the exponential speedup created by applying np methods directly on arrays cannot be matched by function.map, for loops/list comprehensions, or even numpy's own vectorize method.

After like 10 minutes of searching through numpy docs, I found a numpy array method for doing this without list comprehension.

def ssum(bitstring_subset):
    return (bitstring_subset.sum(axis=1) % 2 - 0.5) * -2

Ahhh... so much better.



And after finding a way to vectorize the other list comprehension, this is what the final time looks like:



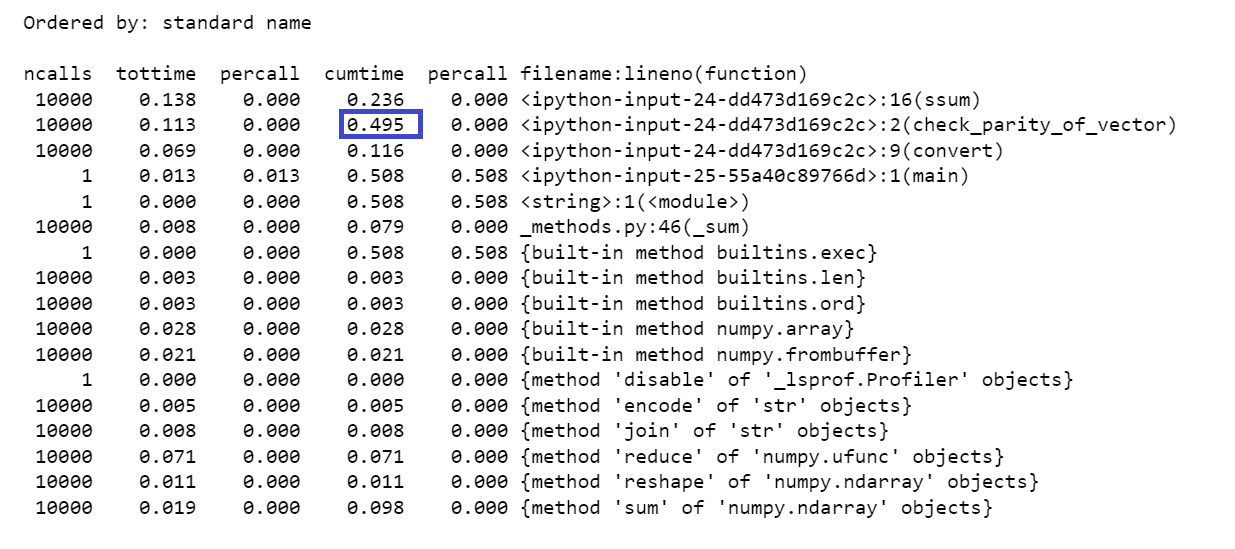
It was also around here that I developed a huge appreciation for how many native array methods numpy has. So, if you think you need to break up an array, chances are, you probably don't.

In the next example, well, I'll let it speak for itself:



This is from the first QAOA I'd ever implemented, for a QOSF mentorship application about a year ago. This piece of code was INSIDE the cost function, or more specifically, inside the function that RAN THE CIRCUIT. Which means that this piece of nausea was run every single time we evaluated the circuit, which is like, a hundred times every optimization run because I set the optimizer to run 100 iterations. This was also part of the code I used for this webapp and combined with many other inefficiencies, it is very slow. You can try it now. I used to blame it on how "quantum computing is just slow," but by now you'd see how wrong that is.

I can't believe I actually wrote this. But I guess a year ago, I wasn't very familiar with numpy. [1] Here's the better way, following the rule that you should keep arrays as arrays while only using built in numpy array methods whenever possible:

gammas = params.reshape(-1, 2).T[0]
betas = params.reshape(-1, 2).T[1]

`np.dot` is magical. In scientific programmming, lots of equations you might want to turn into code have summations over matrix elements like this:



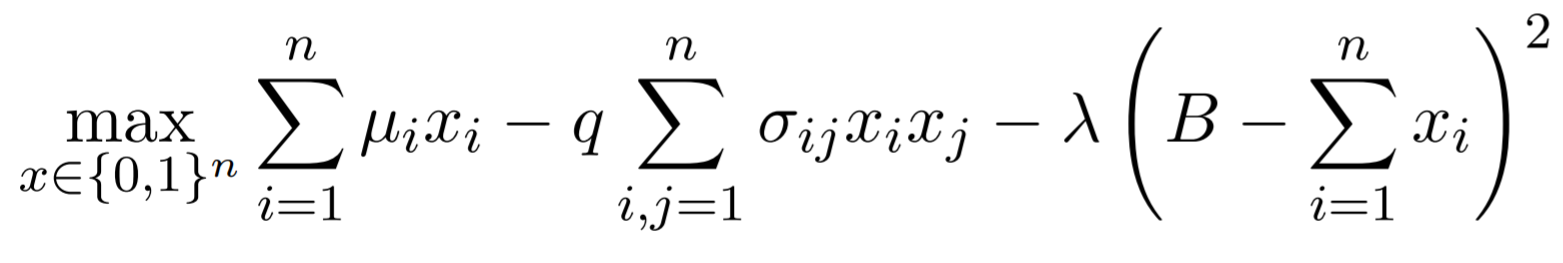
(^formulation of portfolio optimization from here)

where for example, in the second term, you multiply

The default programmer instinct that I had a month ago was to use a for loop.

for i in range(n):
    for j in range(n):
        ...

Instead, though, this is easily achieved by np.dot(x, np.dot(sigma, x)). No loops.

Vectorization rule of thumb #3: In general, math equations in papers can almost always certainly be perfectly vectorized. If there is a

I guess if you're into math you probably intuitively know this, that linear algebra is really cool because it allows you write many arithmetic operations into this nice neat clean equation of the multiplication of two matrices. And that for looping over arrays, the python equivalent of a matrix, is abhorrent because that's not what arrays were intended to do. You're going against the grain of numpy's 20 years of optimizing the efficiency of running large matrix multiplications.



^^Don't let this cutie pie deceive you. It may look like a simple multiplication of 3 things, but it actually involves 1000 separate products and sums. [2]

In conclusion, numpy really is magical. It has brought the beauty of linear algebra into the realm of code, and I think that's really beautiful. [3]

Footnotes:

[1] Although I might be making it sound bad, it's nice how I can look back at code I wrote a year ago and find something I could do better every 5 lines. It does reflect that I'd grown a lot over the past year. Though last year was my first year properly going into software development, so a steep learning curve is to be expected at the beginning. Maybe I should write another post roasting my own code next year :D

[2] Those equations might look neat to mathematician, but to a beginner who doesn't know linear algebra but is trying to implement quantum papers into code, it is a pain to keep track of everything. On top of barely understanding numpy that you use a for loop to do a simple reshape, you have to be thinking, ah yes that

sorry that went a little off topic ;( That TOTALLY wasn't me a year ago and I didn't just rant about it because I still remember the frustration.

But anyway, I'm glad that I'm over that traumatic phase :D Now, I guess I know how to appreciate the beauty of linear algebra and its code counterparts.

[3] Numpy has changed my understanding of linear algebra. I guess I'm weird because I did scientific programming before I learned linear algebra properly, so my understanding of vectors and matrices mostly comes from numpy. For instance, I don't know the mathematical symbol for a matrix transpose so I just write it as .T (the numpy method for transpose). I'm sorry if that made you cringe.

But anyway, what I wanted to say is that before I learned about vectorization, I'd always found linalg just a pain and another way for physics papers to torture me. But numpy has made me see the beauty of matrix multiplications, even if it's only because they make my code run faster and look nicer by having fewer lines.