Loading...

Explore

Postulate is the best way to take and share notes for classes, research, and other learning.

More info
e157: radio frequency circuit design

Lecture 10, 11: Z and S parameters, VNAs

Profile picture of Samson ZhangSamson Zhang
Oct 2, 2023Last updated Oct 3, 20234 min read

Time to generalize to two-port networks!



We're introduced to Z parameters describing how inputs on both ports affect outputs on both ports.

Z parameters

You can solve for Z parameters with this lil Thevenin thing with a dependent source in the imddle.



Specifically, drive port 1 with a current source

I_{t1} It1 I_{t1}
and leave port 2 open. Then:

V_1 = Z_{11} I_1 + Z_{12} I_2 = Z_{11} I_1 \\ V_2 = Z_{22} I_2 + Z_{21} I_1 = Z_{21} I_1
V1=Z11I1+Z12I2=Z11I1V2=Z22I2+Z21I1=Z21I1V_1 = Z_{11} I_1 + Z_{12} I_2 = Z_{11} I_1 \\ V_2 = Z_{22} I_2 + Z_{21} I_1 = Z_{21} I_1

Another way to see this is that

V_{tr1} = 0 Vtr1=0 V_{tr1} = 0
on the port 1 equivalent circuit, so you just get a resistor driven by
I_1 I1 I_1
. And on port 2
I_2 = 0 I2=0 I_2 = 0
, so the entire voltage is caused by
V_{tr2} Vtr2 V_{tr2}
and the resistor
Z_{22} Z22 Z_{22}
has no effect.

Anyways -- with this setup, you can measure

V_1 V1 V_1
to determine
Z_{11} Z11 Z_{11}
and measure
V_2 V2 V_2
to determine
Z_{21} Z21 Z_{21}
. Then, drive port 2 with
I_2 I2 I_2
and leave port 1 open to find
Z_{22} Z22 Z_{22}
and
Z_{12} Z12 Z_{12}
.

Like there are Norton equivalents to Thevenin circuits, so is there a Y parameter equivalent to Z parameters. I hope it's not on the quiz.



S parameters

Z parameters are hard to find at high frequency because it's hard to make a high frequency current source, and also really hard to make a high frequency open circuit, because the open will act as a capacitance. (why? doesn't capacitance decrease with frequency?)

So instead, we define easier to measure S parameters based on ratios of incident and reflected waves, taking into account transmission line effects.



Specifically:

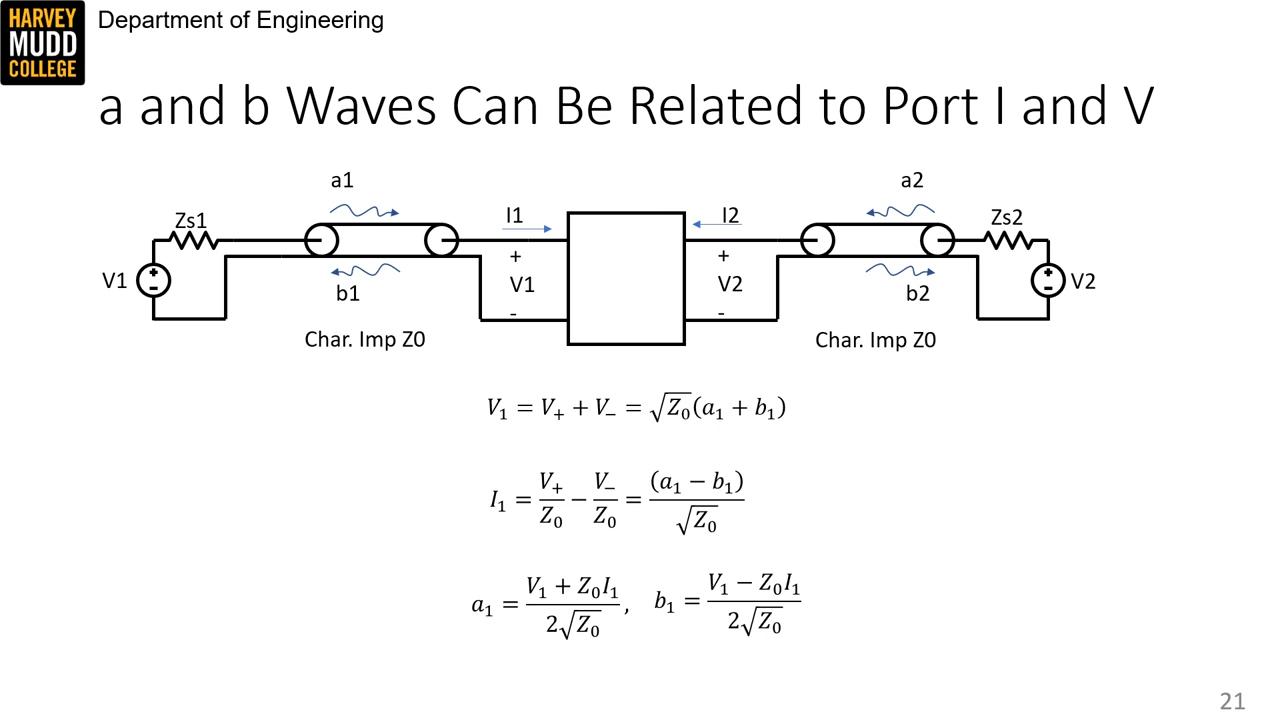
S_{11} = \frac{b_1}{a_1} = \Gamma_1 \big|_\text{2 terminated} \\ S_{22} = \frac{b_2}{a_2} = \Gamma_2 \big|_\text{1 terminated} \\ S_{21} = \frac{b_2}{a_1} = \text{forward gain} \\ S_{22} = \frac{b_1}{a_2} = \text{reverse isolation}
S11=b1a1=Γ1∣2 terminatedS22=b2a2=Γ2∣1 terminatedS21=b2a1=forward gainS22=b1a2=reverse isolationS_{11} = \frac{b_1}{a_1} = \Gamma_1 \big|_\text{2 terminated} \\ S_{22} = \frac{b_2}{a_2} = \Gamma_2 \big|_\text{1 terminated} \\ S_{21} = \frac{b_2}{a_1} = \text{forward gain} \\ S_{22} = \frac{b_1}{a_2} = \text{reverse isolation}

a and b definitions are a little quircky.

a_1 = \frac{|V_{+, 1}|}{\sqrt{Z_0}} a1=∣V+,1∣Z0 a_1 = \frac{|V_{+, 1}|}{\sqrt{Z_0}}
for convenience of power calculation
<P_{+,1}> = \frac{|a_1|^2}{2} <P+,1>=∣a1∣22 <P_{+,1}> = \frac{|a_1|^2}{2}
.



To convert from voltage and current (amplitude of sinusoids), use the following equations:

a_1 = \frac{V_1 + Z_0 I_1}{2\sqrt{Z_0}}, b_1 = \frac{V_1 - Z_0 I_1}{2\sqrt{Z_0}}
a1=V1+Z0I12Z0,b1=V1−Z0I12Z0a_1 = \frac{V_1 + Z_0 I_1}{2\sqrt{Z_0}}, b_1 = \frac{V_1 - Z_0 I_1}{2\sqrt{Z_0}}

Which comes from this derivation:



There's also a helpful general conversion from

S_{11} S11 S_{11}
to
S_{21} S21 S_{21}
:

S_{21} = \frac{V_2}{V_1} (1 + S_{11})
S21=V2V1(1+S11)S_{21} = \frac{V_2}{V_1} (1 + S_{11})

Here's the recap: find

S_{11} S11 S_{11}
as a straightforward reflection coefficient, then get
S_{21} S21 S_{21}
by measuring
V_2 V2 V_2
(amplitude of sinuisoid) and using the conversion formula. Then switch ports to find
S_{22} S22 S_{22}
and
S_{12} S12 S_{12}
.



Fixturing

S parameters can be measured with a vector network analyzer.

First, however, the wires attached to the device being measured -- called fixturing -- must be accounted for, i.e. the reference planes moved to the end of the wire instead of between the wire and the VNA port.

Specifically, transmission lines will add some phase

e^{j(k_1 S_1 + k_2 S_2)} ej(k1S1+k2S2) e^{j(k_1 S_1 + k_2 S_2)}
to the S of the device.



Doing a frequency sweep of each side terminated in a short is one way to determine

kS kS kS
, by looking at the dips in the frequency-gain plot.



A through termination can be used to account for the frequency response of each port, combined

H_1(j\omega) H_2(j\omega) H1(jω)H2(jω) H_1(j\omega) H_2(j\omega)
(as generic transfer functions).



Directional couplers and VNAs

How does a VNA actually measure forward and reverse waves? With a directional coupler:



Signal going into input goes to the through port,

b_2 = a_1 b2=a1 b_2 = a_1
. Signal going into through goes to input as well,
b_1 = a_2 b1=a2 b_1 = a_2
, but also to "coupled",
b_4 = C * a_2 b4=C∗a2 b_4 = C * a_2
. There is some leakage from
a_1 a1 a_1
, so in practice
b_4 = C * a_2 + \epsilon * a_1 b4=C∗a2+ϵ∗a1 b_4 = C * a_2 + \epsilon * a_1
.

A VNA looks like this:



The above slide shows errors that arise if

Z_s \neq Z_0 Zs≠Z0 Z_s \neq Z_0
.

Source mismatch can be calibrated for with an open termination, while finite directivity can be calibrated for with a load. With the short and through calibrations above, these make up SOLT calibration, which can be done manually or with something called ECal.

There are different calibrations when the device is attached to a board instead of wires, such as through-reflect-line (TRL) and line-reflect-match (LRM).

Calibrations are specific to a frequency range and cable, and also sensitive to the temperature of the VNA.

Comments (loading...)

Sign in to comment

e157: radio frequency circuit design

fall 2023 class w prof. spencer