Video Set 5A: Control Systems!

Say you have some system and you want the system's output to be some

If you have a perfect model of the system, you can solve analytically for the

Often, though, your model will be imperfect, and the output will be off from what you want it to be. In this case, you can add a feedback loop, or use "closed loop control." The block diagram for closed loop control looks like this:



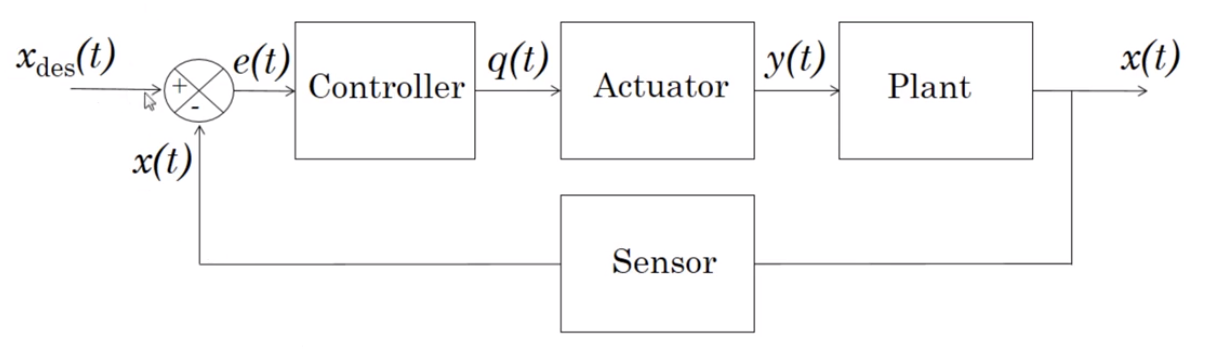
Block diagrams

A block just represents a signal being processed by a transfer function. In the diagram below,



You can do some nice things with blocks. If they are in series, you can combine them, i.e. for the below diagram



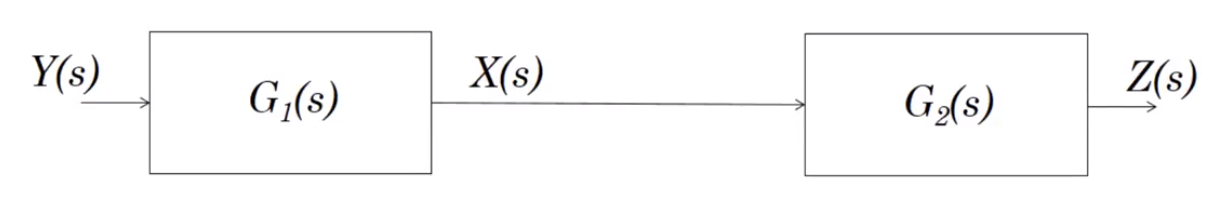
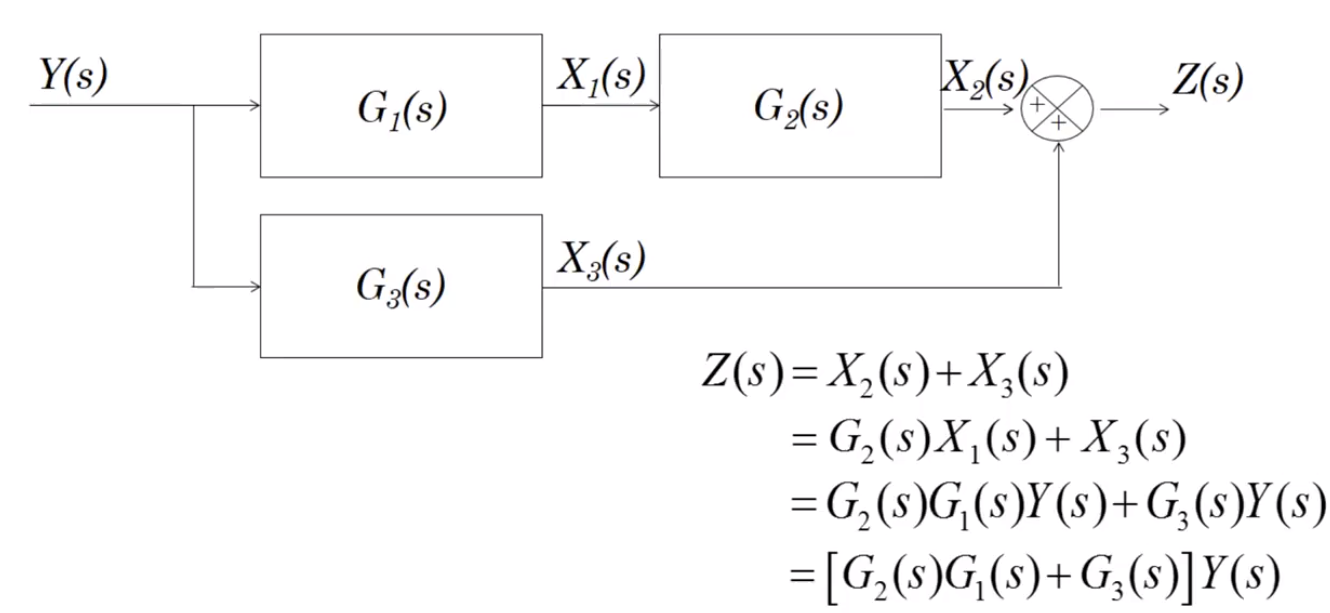
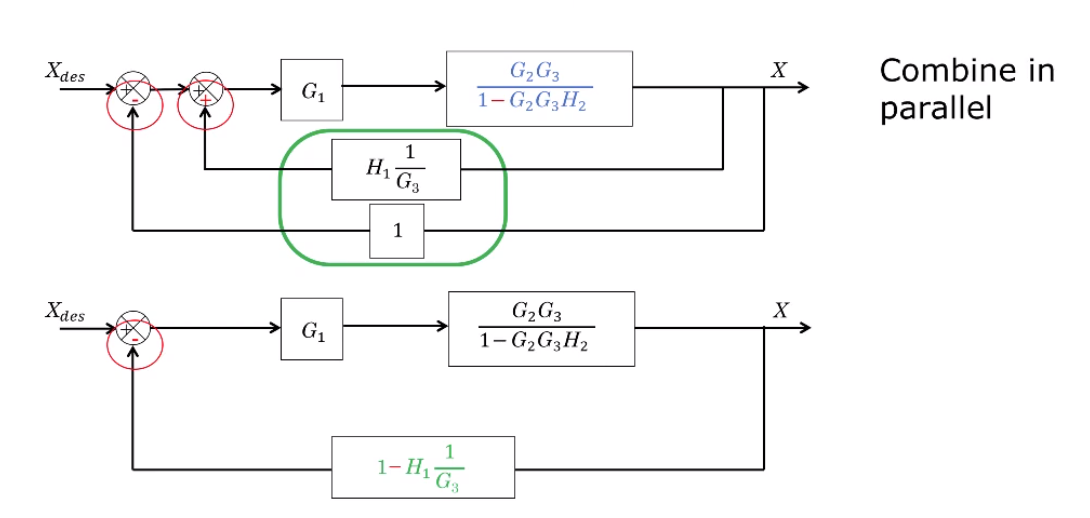
Parallel branches can be summed together by a sum symbol:



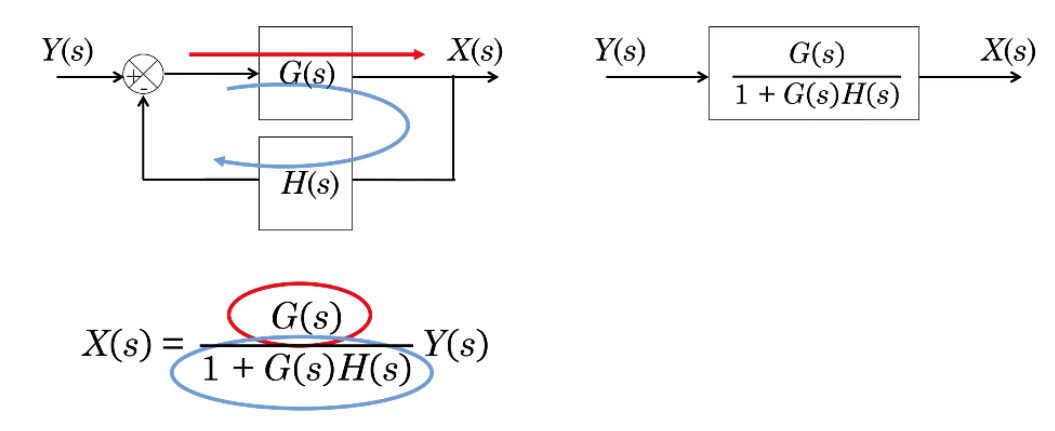
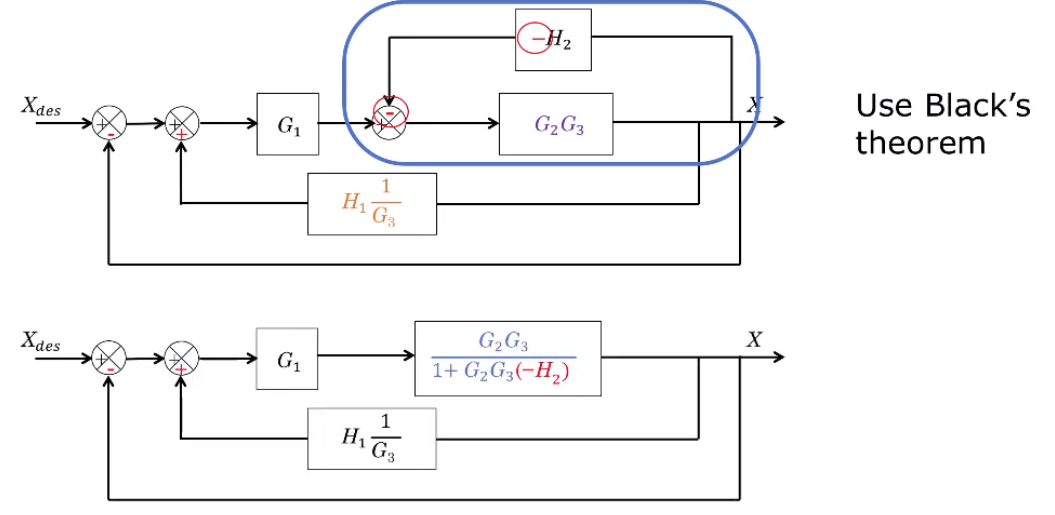
Finally, "Black's theorem" tells us that in a feedback loop, the equivalent block has transfer function



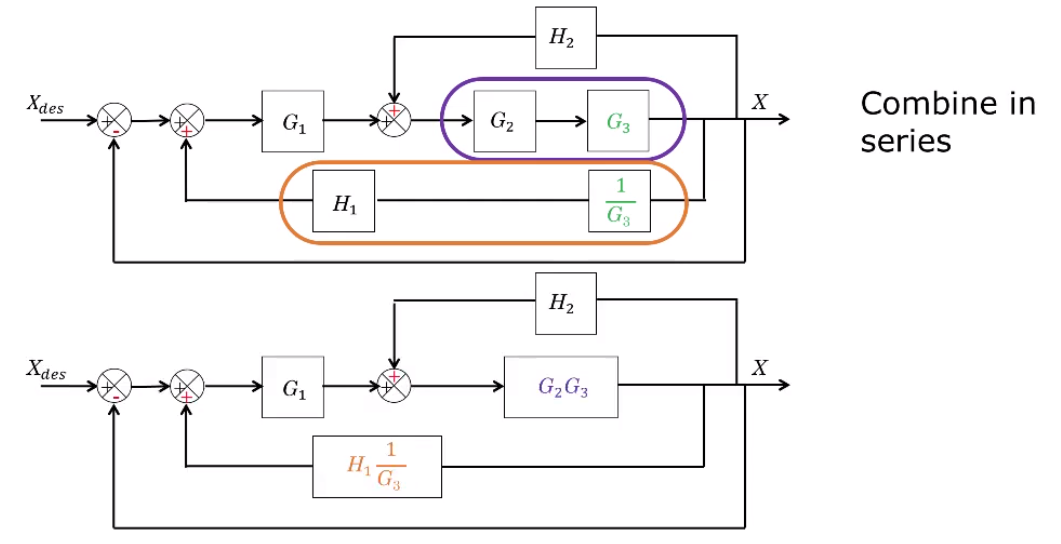
In some block diagrams, the above tools rae not enough to simplify blocks, as in the below example:



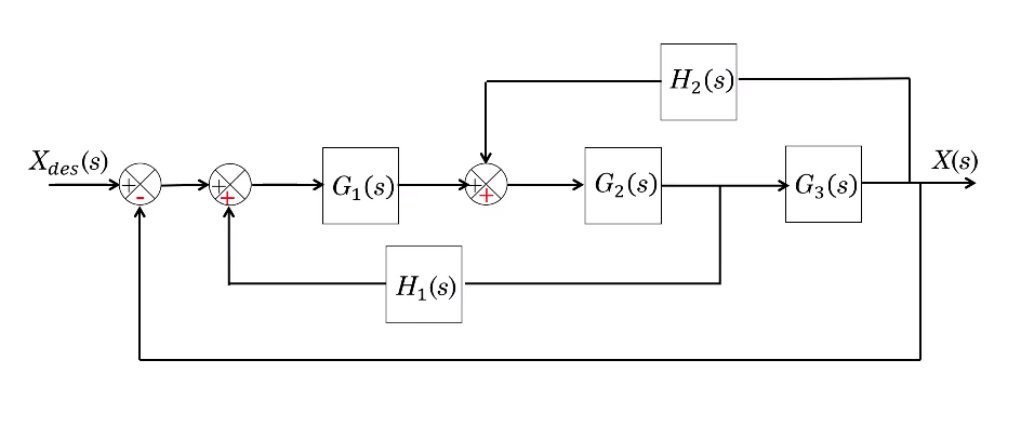
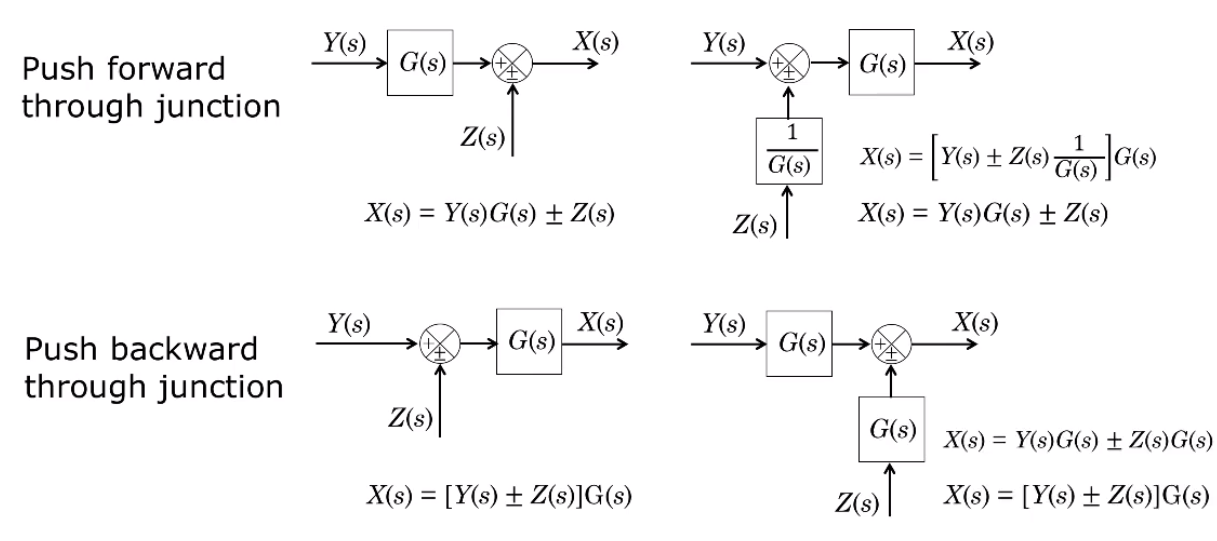
In this case we can use something called "block pushing", moving blocks before and after junctions in ways that preserve the transfer function to make them combinable:



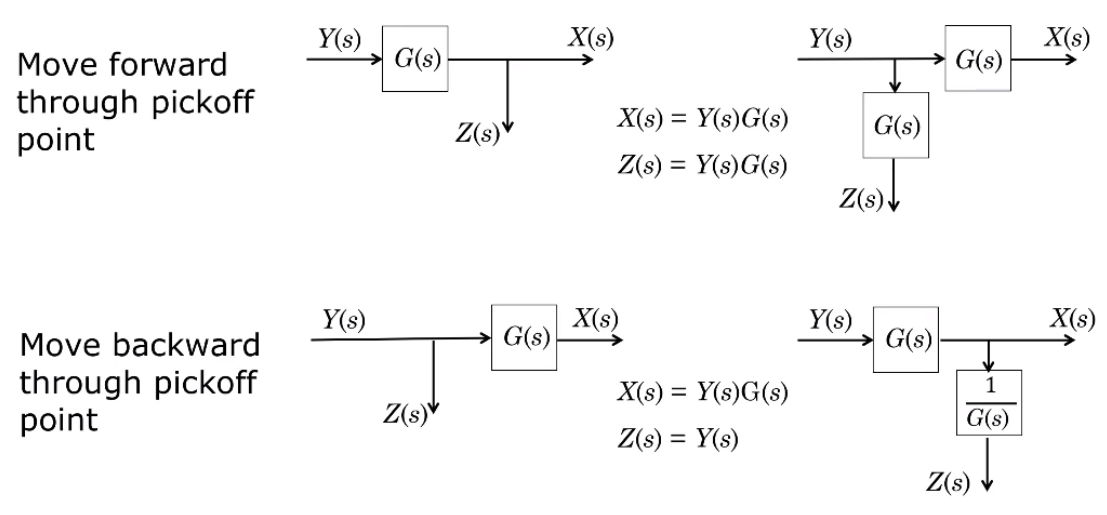
This can also be done through pickoff points:



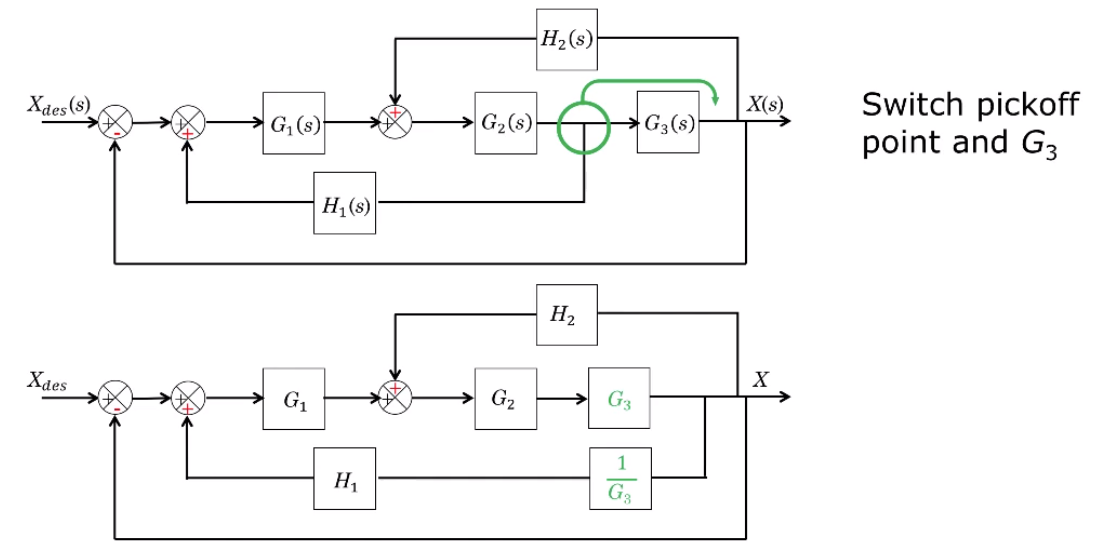
Using these block pushing techniques we can simplify the earlier diagram:











Bang bang and P control

Now, back to controllers. There are a bunch of different controllers:



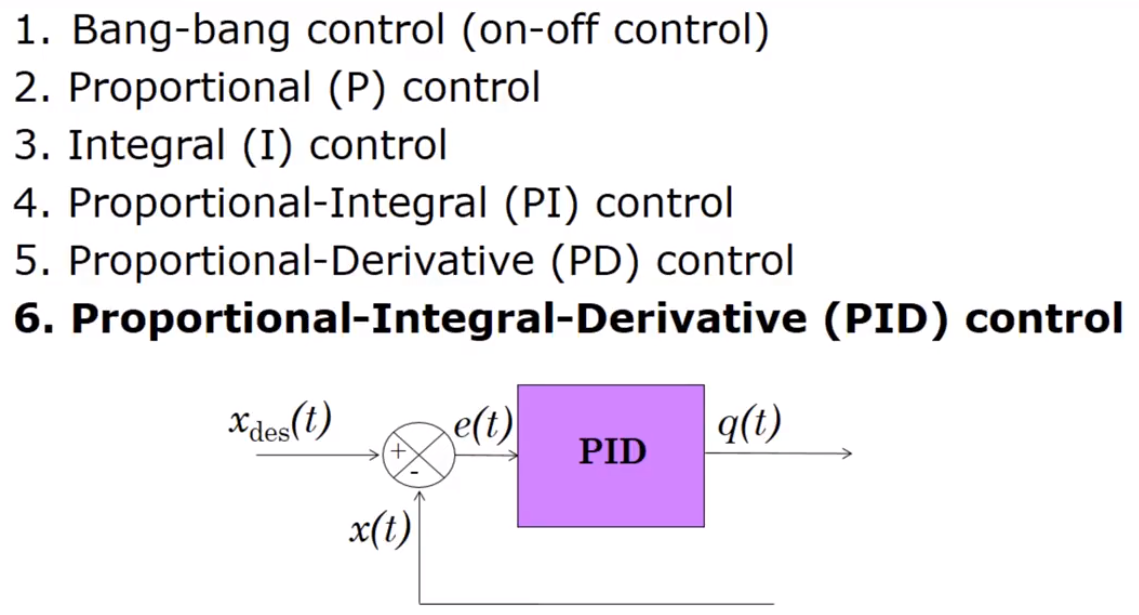
Bang-bang control simply turns the system on or off at certain thresholds:



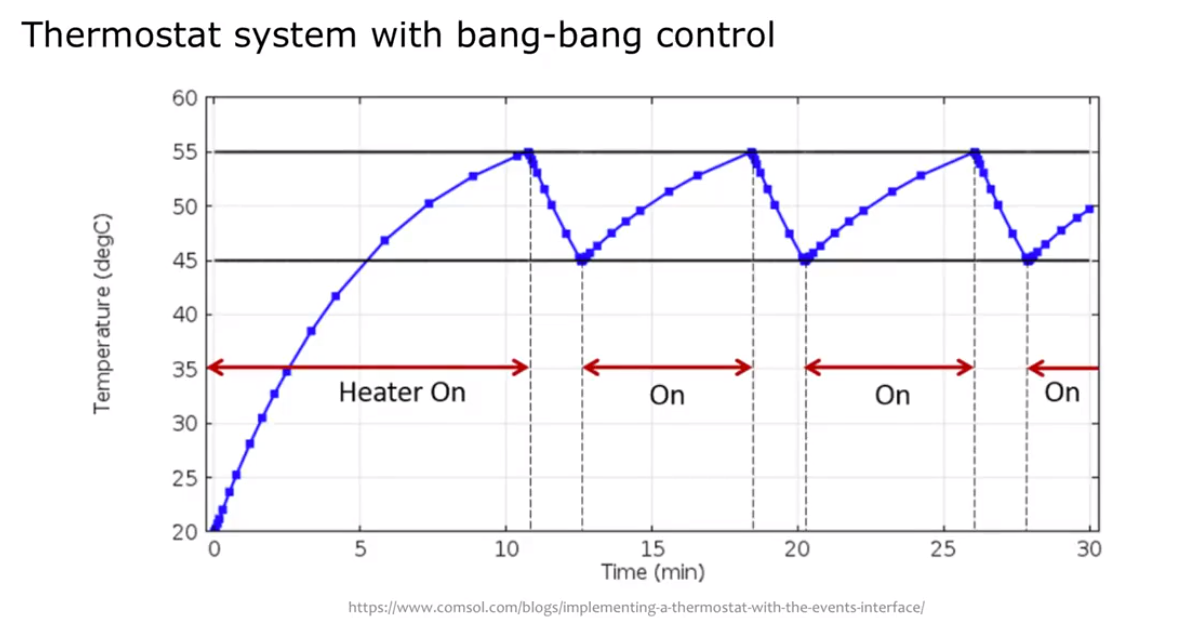
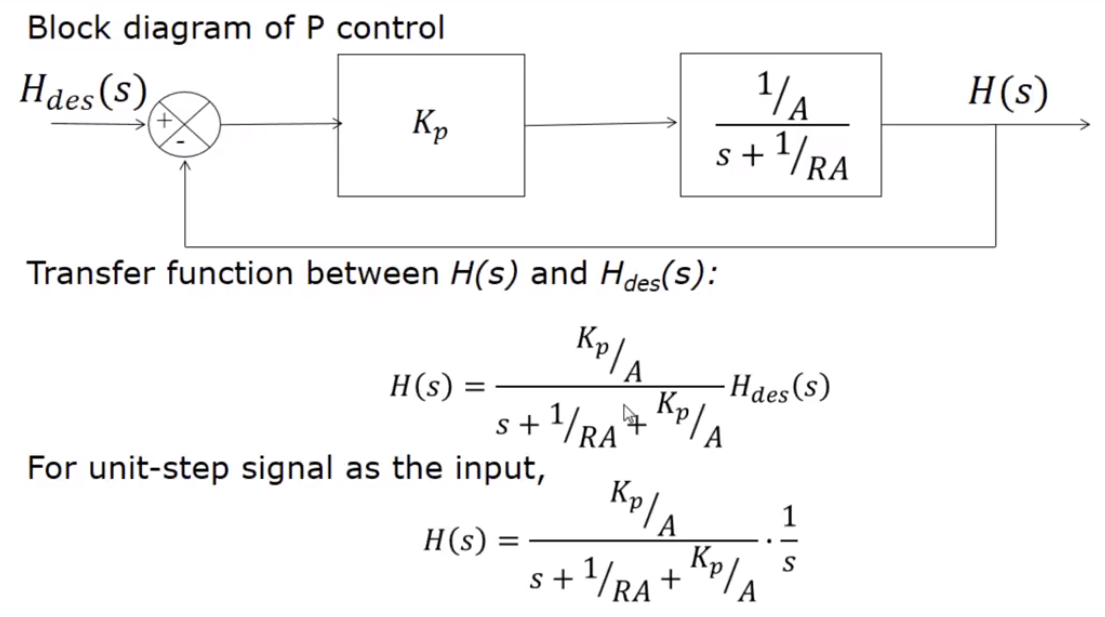
Proportional control, on the other hand, applies an input with gain proportional to the error between output and desired output with the coefficient



P control can be analyzed with a transfer function relating