Loading...

Explore

Postulate is the best way to take and share notes for classes, research, and other learning.

More info
E79: Engineering Systems

Tutorial: Hovercraft control system example

Profile picture of Samson ZhangSamson Zhang
Nov 26, 20224 min read

A tutorial problem that really helped me get an intuition for content from 5A!

Consider this hovercraft:



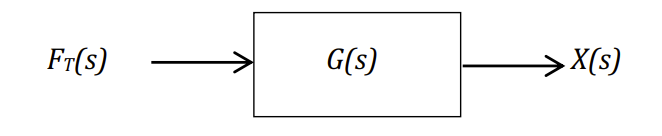
Naively, we can represent the hovercraft through a simple block diagram:



To get a certain

X_\text{des}(s) Xdes(s) X_\text{des}(s)
, we can solve for a
G_O(s) GO(s) G_O(s)
block to get
F_T(s) FT(s) F_T(s)
:



The solution is straightforward:

X = G_O G X_\text{des} \\ \implies G_O = \frac{1}{G} = ms^2 + bs
X=GOGXdes  ⟹  GO=1G=ms2+bsX = G_O G X_\text{des} \\ \implies G_O = \frac{1}{G} = ms^2 + bs

The problem with this control system -- known as "open loop" control because there is no feedback cycle -- is that it has no resistance to error.

Consider an unaccounted-for wind force

W(s) W(s) W(s)
acting on the system:



Now the behavior of the entire system is:

\begin{align*} X &= G(W + F_T) \\ &= G(W + G_O X_\text{des}) \\ &= GW + G G_O X_\text{des} \\ &= GW + X_\text{des} \\ \end{align*}
X=G(W+FT)=G(W+GOXdes)=GW+GGOXdes=GW+Xdes\begin{align*} X &= G(W + F_T) \\ &= G(W + G_O X_\text{des}) \\ &= GW + G G_O X_\text{des} \\ &= GW + X_\text{des} \\ \end{align*}

Consider the final value of this system using the final value theorem for some step input

W(s) = \frac{W_\text{in}}{s} W(s)=Wins W(s) = \frac{W_\text{in}}{s}
:

\begin{align*} \lim_{t\to\infty} x(t) &= \lim_{s\to 0} s(X(s)) \\ &= \lim_{s\to 0} s(GW + X_\text{des}(s)) \\ &= \lim_{s\to 0} s\bigg(\frac{1}{ms^2 + bs} \frac{W_\text{in}}{s} + X_\text{des}(s)\bigg) \\ &= \lim_{s\to 0} \frac{1}{ms^2 + bs} W_\text{in} + X_\text{des}(s)s \\ \end{align*}
lim⁡t→∞x(t)=lim⁡s→0s(X(s))=lim⁡s→0s(GW+Xdes(s))=lim⁡s→0s(1ms2+bsWins+Xdes(s))=lim⁡s→01ms2+bsWin+Xdes(s)s\begin{align*} \lim_{t\to\infty} x(t) &= \lim_{s\to 0} s(X(s)) \\ &= \lim_{s\to 0} s(GW + X_\text{des}(s)) \\ &= \lim_{s\to 0} s\bigg(\frac{1}{ms^2 + bs} \frac{W_\text{in}}{s} + X_\text{des}(s)\bigg) \\ &= \lim_{s\to 0} \frac{1}{ms^2 + bs} W_\text{in} + X_\text{des}(s)s \\ \end{align*}

Remember that

X_\text{des}(s) Xdes(s) X_\text{des}(s)
is not itself a constant. If
x_\text{des}(t) xdes(t) x_\text{des}(t)
is a constant,

X_\text{des}(s) Xdes(s) X_\text{des}(s)

is the Laplace transform of the constant, with the value
\frac{x_\text{const}}{s} xconsts \frac{x_\text{const}}{s}
. In the above limit, then,
X_\text{des}(s)s = \frac{x_\text{const}}{s}s = x_\text{const} Xdes(s)s=xconstss=xconst X_\text{des}(s)s = \frac{x_\text{const}}{s}s = x_\text{const}
-- absent wind, the final value is just the desired value, as expected.

The first term, on the other hand, has a denominator that goes to 0. Unless

W_\text{in} = 0 Win=0 W_\text{in} = 0
, the entire term will thus blow up to infinity.

And that makes sense! Wind error is entirely uncorrected for, so the hovercraft will drift farther and farther off of its desired path over time.

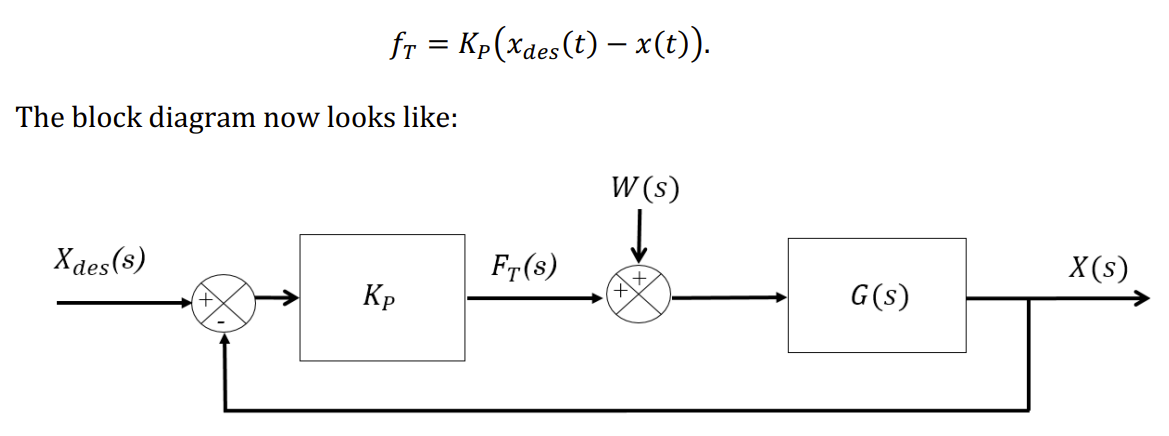
To fix this, let's replace open loop control with proportional control. That is, we'll swap out the

G_O GO G_O
block for a
K_P KP K_P
block and a node for calculating error:



Now the system behavior can be characterized by the following equation:

\begin{align*} X &= G(W + F_T) \\ &= G(W + K_P (X_\text{des} - X)) \\ \implies X &= \frac{G}{1+K_P G}W + \frac{K_P G}{1+K_P G}X_\text{des} \\ \end{align*}
X=G(W+FT)=G(W+KP(Xdes−X))  ⟹  X=G1+KPGW+KPG1+KPGXdes\begin{align*} X &= G(W + F_T) \\ &= G(W + K_P (X_\text{des} - X)) \\ \implies X &= \frac{G}{1+K_P G}W + \frac{K_P G}{1+K_P G}X_\text{des} \\ \end{align*}

Once again we have a term for wind and one for control.

Let's take a look at the final value of the control term:

\begin{align*} x_\text{final, control} &= \lim_{s\to0} s \frac{K_P G}{1+K_P G}X_\text{des} \\ &= \lim_{s\to0} s \frac{K_P \frac{1}{ms^2 + bs}}{1 + K_P \frac{1}{ms^2 + bs}} X_\text{des} \\ &= \lim_{s\to0} s \frac{K_P}{ms^2 + bs + K_P} X_\text{des} \\ \end{align*}
xfinal, control=lim⁡s→0sKPG1+KPGXdes=lim⁡s→0sKP1ms2+bs1+KP1ms2+bsXdes=lim⁡s→0sKPms2+bs+KPXdes\begin{align*} x_\text{final, control} &= \lim_{s\to0} s \frac{K_P G}{1+K_P G}X_\text{des} \\ &= \lim_{s\to0} s \frac{K_P \frac{1}{ms^2 + bs}}{1 + K_P \frac{1}{ms^2 + bs}} X_\text{des} \\ &= \lim_{s\to0} s \frac{K_P}{ms^2 + bs + K_P} X_\text{des} \\ \end{align*}

For a constant

X_\text{des} = \frac{x_\text{const}}{s} Xdes=xconsts X_\text{des} = \frac{x_\text{const}}{s}
,
x_\text{final, control} = \frac{K_P}{K_P} X_\text{des} = X_\text{des} xfinal, control=KPKPXdes=Xdes x_\text{final, control} = \frac{K_P}{K_P} X_\text{des} = X_\text{des}
, as expected. We can also note that this system has a second-order transfer function: for a step response
X_\text{des} Xdes X_\text{des}
, we can expect an output that rises exponentially to the steady state value, possibly overshooting depending on
\zeta ζ \zeta
.

Now let's look at wind for step input

W(s) = \frac{w_\text{in}}{s} W(s)=wins W(s) = \frac{w_\text{in}}{s}
:

\begin{align*} x_\text{final, wind} &= \lim_{s\to0} s \frac{G}{1+K_P G}W \\ &= \lim_{s\to0} s \frac{\frac{1}{ms^2 + bs}}{1 + K_P \frac{1}{ms^2 + bs}} \frac{w_\text{in}}{s} \\ &= \lim_{s\to0} \frac{w_\text{in}}{ms^2 + bs + K_P} \\ &= \frac{w_\text{in}}{K_P} \end{align*}
xfinal, wind=lim⁡s→0sG1+KPGW=lim⁡s→0s1ms2+bs1+KP1ms2+bswins=lim⁡s→0winms2+bs+KP=winKP\begin{align*} x_\text{final, wind} &= \lim_{s\to0} s \frac{G}{1+K_P G}W \\ &= \lim_{s\to0} s \frac{\frac{1}{ms^2 + bs}}{1 + K_P \frac{1}{ms^2 + bs}} \frac{w_\text{in}}{s} \\ &= \lim_{s\to0} \frac{w_\text{in}}{ms^2 + bs + K_P} \\ &= \frac{w_\text{in}}{K_P} \end{align*}

We find that there is still an error, but the error is finite now, and smaller the higher

K_P KP K_P
is. This error also has a second-order step response.

A nice example of proportional control and the math behind it!

Comments (loading...)

Sign in to comment

E79: Engineering Systems

Notes for e79 w Prof. Shia at HMC in fall 2022